Poder Estatístico - Uma abordagem compreensiva
Nota prévia: Neste artigo, usarei alguns códigos apresentados pelos professores João Veríssimo e Audrey Bürki durante o último SMLP - Fifth Summer School on Statistical Methods for Linguistics and Psychology. Fiz apenas algumas modificações a fim de tonar a apresentação aqui mais didática.
Nível de significância e poder do teste
Quando se trata do clássido teste de hipóteses do paradigma frequentista (NHST - Null Hyphotesis Significance Testing… o que exatamente isso quer dizer já é em si uma questão. Não deixe de ler Perezgonzalez (2015) para uma abordagem extramente didática), as opções que temos para lidar com a relação entre rejeição ou não da Hipótese Nula (H0) estão resumidas na tabela abaixo:
| Decisão | H0 é verdadeira (não existe efeito) | H0 é falsa (existe um efeito) |
|---|---|---|
| Rejeitar | Falso Positivo | Decisão correta |
| (Erro do Tipo I ou alpha) | (verdadeiro positivo ou 1 - beta) | |
| Não Rejeitar | Decisão correta | Falso negativo |
| (Verdadeiro negativo ou 1 - alpha) | (Erro do Tipo II ou beta) |
A probabilidade de cometermos um Erro do Tipo I, ou seja, de anunciarmos um efeito quando ele na verdade não existe é chamada de nível de significância (no, digamos assim, paradigma “fisheriano”) ou alpha (no paradigma de Neyman-Pearson) e é um valor arbitrário, convencionalmente estabelecido (em psicolinguística, geralmente de 0.05 ou 5%). A probabilidade de cometermos um Erro do Tipo II, ou seja, de não descobrirmos um efeito quando ele de fato existe é denominada beta e seu valor complementar (1 - beta) é o chamado poder do teste, ou seja, é a probabilidade de decobrirmos um efeito quando ele de fato existe. Esse valor é dependente:
- (i) do tipo de teste que estamos aplicando;
- (ii) do tamanho do efeito que estamos mensurando;
- (iii) do tamanho da amostra que temos; e
- (iv) do nível de significância.
O que nós vamos fazer aqui é tentar entender o que são alpha (ou nível de significância) e beta (ou poder do teste) com base em algumas simulações computacionais.
IMPORTANTE: o trabalho com simulações tem muito mais efeito pedagógico se você mesmo puder implementá-las no seu computador, neste caso, por meio do R. Para isso, você deveria baixar o script para executar os códigos e acompanhar o debate aqui realizado executando os códigos por si próprio.
Vamos às simulações!
Esse código serve apenas para carregar os pacotes necessários à análise!
require(mvtnorm)
require(ggplot2)
require(dplyr)Poder do teste por meio de simulações
Já que o poder do teste depende do teste que estamos usando, vamos começar com um dos mais simples, o teste-t para dados pareados ou paired t-test. Neste caso, estamos assumindo que os dois grupos comparados são correlacionados. Você pode pensar, por exemplo, que colocamos os mesmos sujeitos para ver ambas as condições experimentais.
Para isso, vamos criar uma função chamada poder.paired, cujos argumentos são explicados abaixo, e carregá-la no R.
O que essa função faz? Nós inserimos nela alguns argumentos que definem as propriedades dos dados que criaremos e ela então retira um grande número de amostras aleatórias com essas propriedades e, para cada uma dessas amostras, calcula um teste-t. Ela então computa qual a proporção desses testes deram significativo, plotando um gráfico da distribuição de frequência desses p-valores.
Em outras palavras, nós damos à função os parâmetros populacionais (que na vida real são desconhecidos, mas que na simulação nós sabemos, porque nós inventamos) e ela retira amostras aleatórias dessa população.
A função já está pronta abaixo. Basta apenas carregá-la no R.
poder.paired <- function(n, mu1, mudiff, sigma1, sigma2, rho12, nsims){
nsims = nsims
# vetor vazio para armazenar os valores de p
pvalor <- c()
for(i in 1:nsims){
n = n
mu1 = mu1
mudiff = mudiff
sigma1 = sigma1
sigma2 = sigma2
rho12 = rho12
mu2 <- mu1 + mudiff # define a média da segunda condição
# Definir a matriz de covariância
cov12 <- rho12 * sigma1 * sigma2
vcov <- matrix(c(sigma1^2, cov12,
cov12, sigma2^2), nrow=2, byrow=T)
# Realizandoo procedimento de amostragem
head(Y <- rmvnorm(n, c(mu1, mu2), vcov))
Y1 <- Y[, 1]
Y2 <- Y[, 2]
test <- t.test(Y2, Y1, paired = T)
pvalor <- c(pvalor, test$p.value)
}
dados <- as.data.frame(pvalor)
poder <- dados %>%
summarise(poder = sum(pvalor < 0.05) / nsims)
ggplot() +
geom_density(data = dados, aes(x = pvalor), fill = "orange", color = "orange", alpha = 0.4) +
geom_vline(aes(xintercept = 0.05), color = "red", linetype = "dashed") +
geom_text(data = poder, aes(label = poder, x = 0.05, y = 0.2)) +
theme_classic() +
labs(x = "p-valor", y = "Densidade")
}Entendendo a função que criamos
Você terá que definir 7 argumentos para essa função, conforme explicados abaixo:
n: o tamanho da amostra desejada.mu1: a média do grupo 1.mudiff: a diferença entre a média do grupo 1 e a média do grupo 2 com o qual comparar o grupo 1. Se esse valor for igual a zero, então os grupos têm médias idênticas e não existe efeito.sigma1esigma2: os desvios padrão dos grupo 1 e 2, que estão sendo comparados.rho12: um valor entre zero e 1 que indica a correlação entre as duas condições. Como os dados são pareados, ou seja, não independentes, então eles serão correlacionados.nsims: número de simulações a serem implementadas (número de amostras que serão retiradas e número de testes t que serão aplicados). O ideal é que seja um valor alto, como 1000 ou 10000.
Exemplo 1: H0 é verdadeira e não há efeito
Vamos começar imaginando um cenário em que os grupos comparados têm médias idênticas, ou seja, mudiff = 0. Em outras palavras, não há efeito na população e H0 é verdadeira.
poder.paired(n = 30,
mu1 = 150,
mudiff = 0,
sigma1 = 40,
sigma2 = 40,
rho12 = 0.3,
nsims = 1000)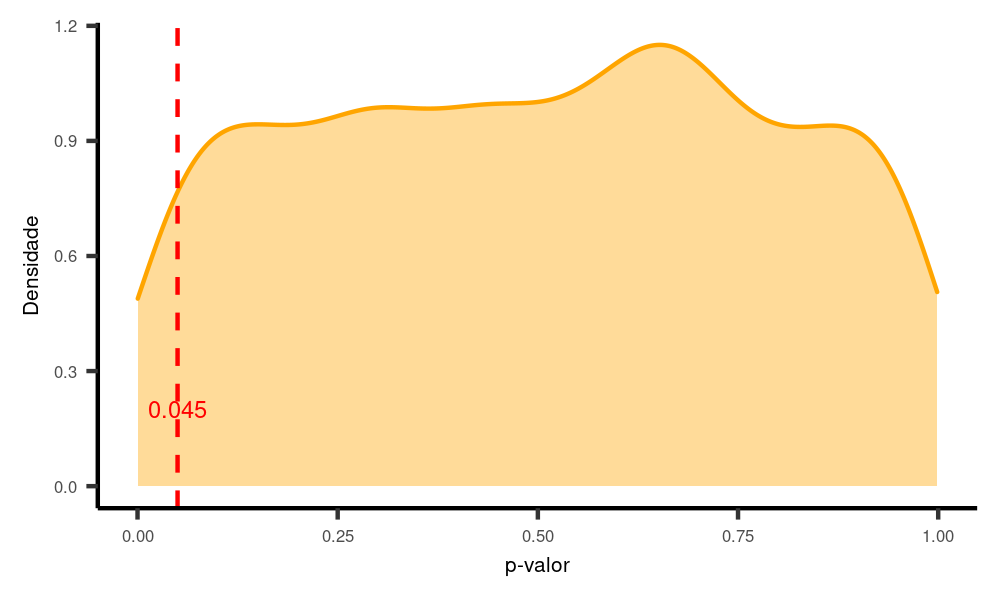
Nesse caso, como mudiff = 0, então H0 é mesmo verdadeira e o poder do teste não se aplica, já que poder é a probabilidade de encontrar um efeito quando ele de fato existe (H0 é falsa). Logo, o que se aplica é o nível de significância. Como se pode ver, apenas cerca de 5% dos nossos resultados são menores do que 0.05 (são falsos positivos). De fato, essa é a definição de p-valor: um p-valor menor do que 0.05 apenas indica que, se replicássemos o experimento um número grande de vezes, obteríamos um efeito significativo em apenas 5% dos casos.
Rode mais algumas vezes o mesmo código acima e veja como esse valor oscila em torno de 5%, às vezes para mais, às vezes para menos.
Exemplo 2: H0 é falsa e existe um efeito pequeno
Aqui temos um efeito de 20 unidades (mudiff = 20), sendo que todos os outros parâmetros foram mantidos constantes.
poder.paired(n = 30,
mu1 = 150,
mudiff = 20, # A única coisa que mudamos foi a diferença entre os grupos
sigma1 = 40,
sigma2 = 40,
rho12 = 0.3,
nsims = 1000)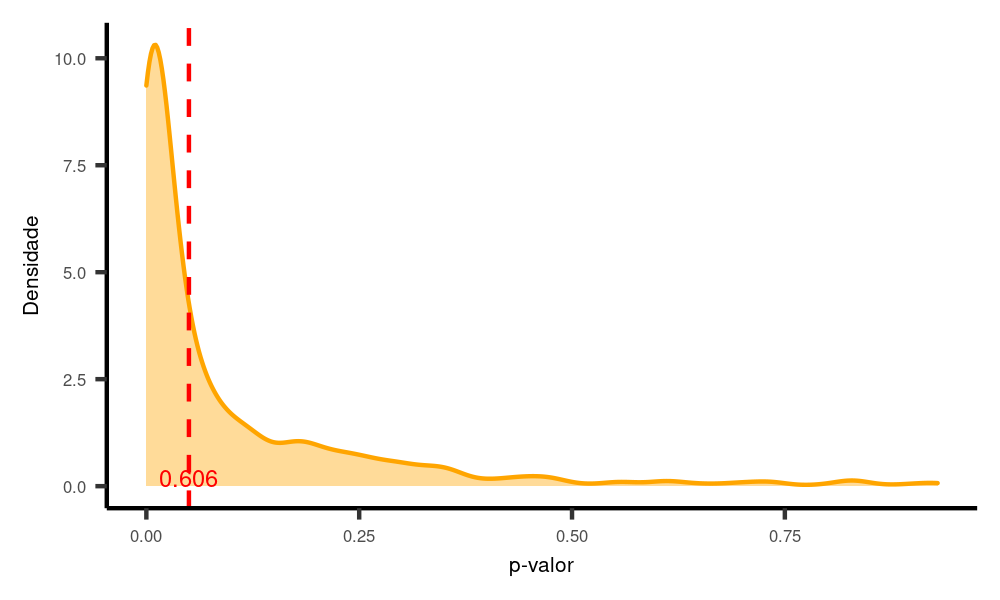
Nesse caso, cerca de 60% dos nossos testes deram significativo (ou seja, são verdadeiros positivos), mas o restante deles (cerca de 40%) foi maior do que 0.05 (falsos negativos). Nestes últimos casos, nós não rejeitaríamos a hipótese nula mesmo sendo ela verdadeira.
Exemplo 3: H0 é falsa e o efeito é maior
Vamos manter tudo igual, mas agora vamos aumentar o tamanho do efeito de 20 para 40:
poder.paired(n = 30,
mu1 = 150,
mudiff = 40, # Mais uma vez, mudamos aqui, agora de 20 para 40
sigma1 = 40,
sigma2 = 40,
rho12 = 0.3,
nsims = 1000)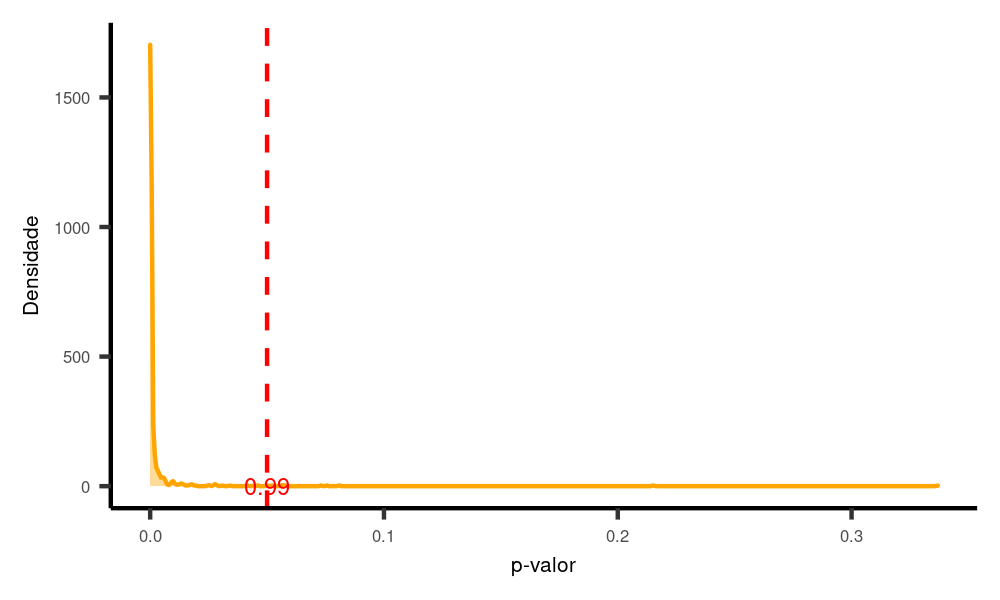
Nesse caso, com um efeito maior, mais testes obtêm resultados positivos, agora próximo dos 100%. Aumentando o tamanho do efeito, aumenta-se o poder.
Exemplo 4: H0 é falsa e a amostra é pequena
Vamos voltar para o nosso Exemplo 2.
Nesse caso, nossa diferança era de 20 e a amostra era de tamanho 30 (n = 30), caso em que tínhamos um poder de cerca de 60%. Vamos reduzi-la para 10, mantendo o restante igual.
poder.paired(n = 10, # Dessa vez, mudamos o tamnho da amostra
mu1 = 150,
mudiff = 20,
sigma1 = 40,
sigma2 = 40,
rho12 = 0.3,
nsims = 1000)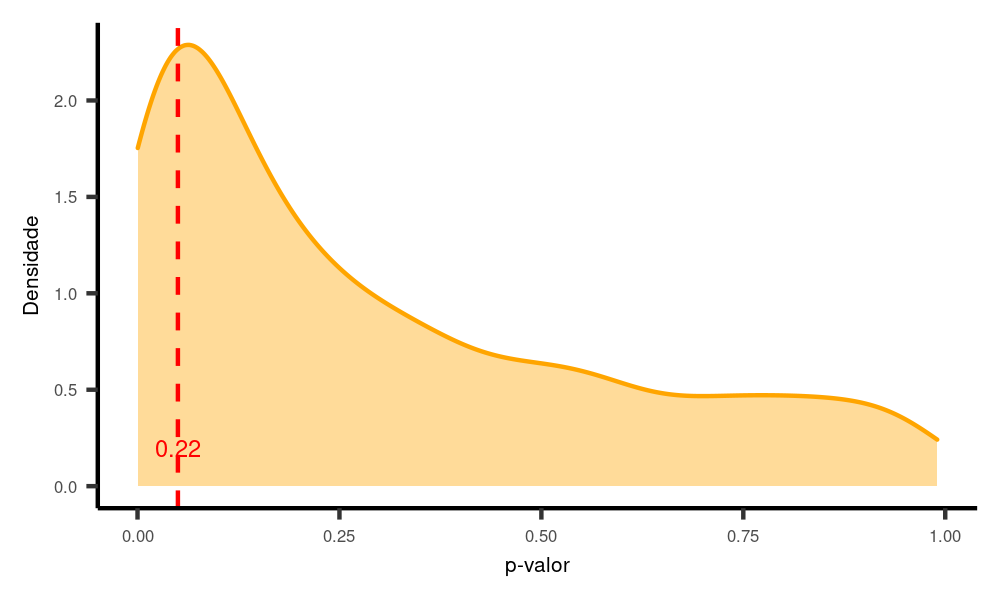
Como você pode ver, ao reduzir o tamanho da amostra, reduzimos drasticamenteo poder do teste (para cerca de 20%). Isso significa que, mesmo que o efeito exista na população, nós só o descobriríamos 20% das vezes que o testássemos!
Exemplo 5: H0 é falsa e a amostra é grande
Se aumentamos o número da amostra para 60, mantendo tudo igual, então aumentamos nosso poder:
poder.paired(n = 60, # Agora aumentando o tamanho da amostra
mu1 = 150,
mudiff = 20,
sigma1 = 40,
sigma2 = 40,
rho12 = 0.3,
nsims = 1000)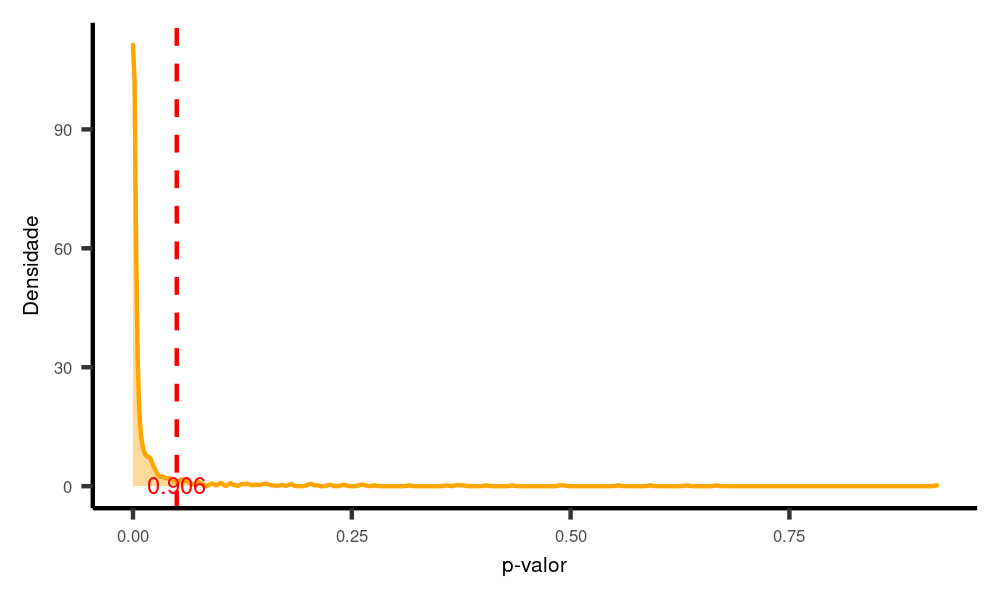
Exemplo 6: Desvio padrão
A variabilidade contida nos dados também afeta o poder do teste (mas, sobre essa, em geral não temos controle).
Mas vamos brincar um pouco aqui: deixemos tudo como o Exemplo 5, acima, mas dobremos o desvio padrão de ambos os grupos (de 40 para 80).
poder.paired(n = 60,
mu1 = 150,
mudiff = 20,
sigma1 = 80, # Agora estamos brincando com a variabilidade dos dados
sigma2 = 80, # E aqui também.
rho12 = 0.3,
nsims = 1000)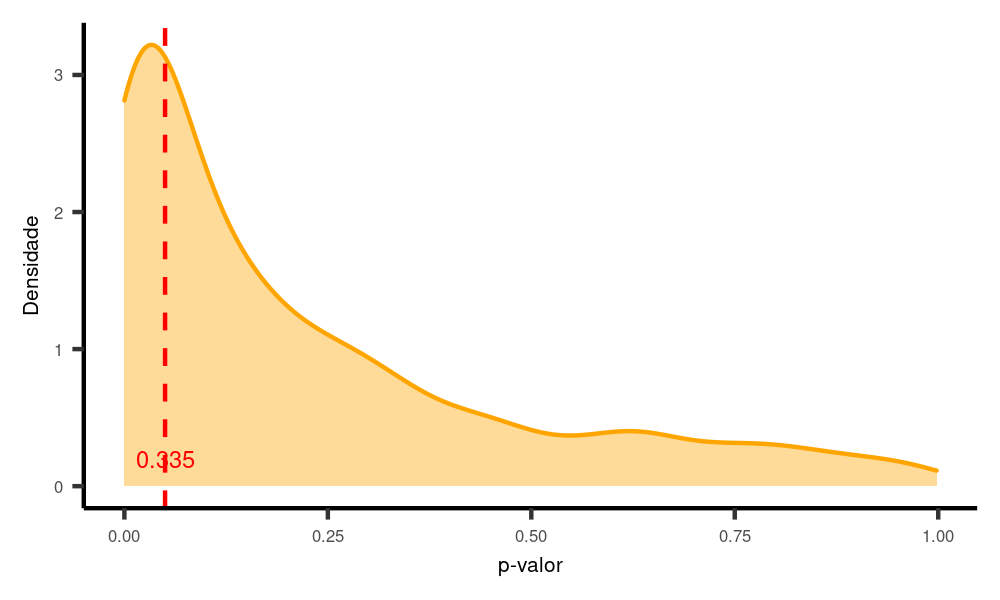
Observe que, com isso, há uma redução do poder do teste. Se há muita variabilidade nos dados (proporcionalmente ao tamanho do efeito), então temos mais dificuldade de encontrar um efeito significativo, mesmo quando ele existe na população.
O contrário ocorre se reduzimos o desvio padrão, digamos, para a metade do que estava antes (de 40 para 20). E vamos reduzir também o tamanho da amostra, para 10, como no Exemplo 4, em que tínhamos cerca de 20% de poder.
poder.paired(n = 10, # Estamos comparando com o exemplo 4!!!
mu1 = 150,
mudiff = 20,
sigma1 = 20, # Agora mudamos aqui, mas reduzindo, dessa vez.
sigma2 = 20, # Aqui também.
rho12 = 0.3,
nsims = 1000)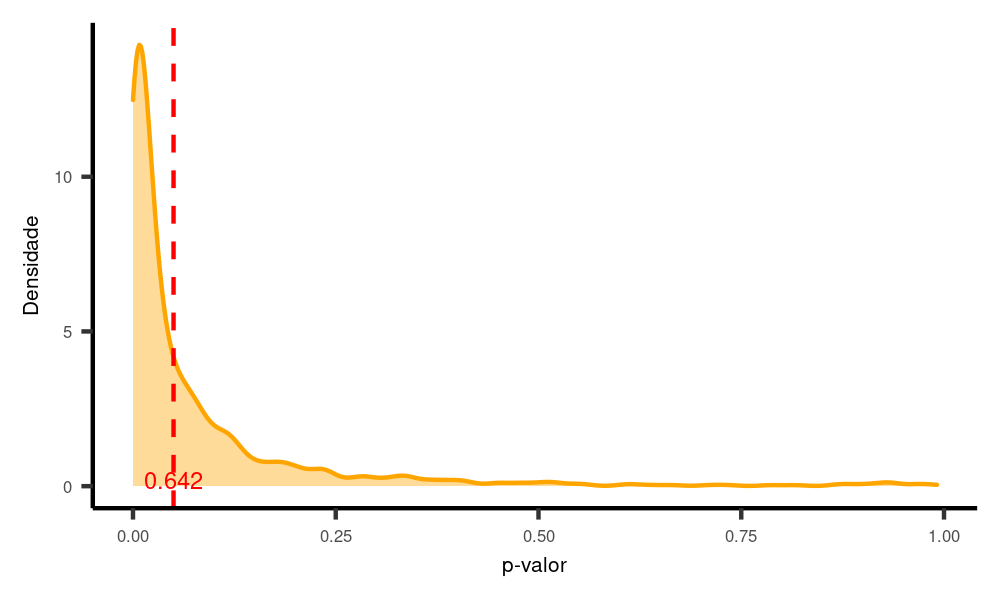
Nesse caso, o poder passou de cerca de 20% no exemplo 4 para cerca de 65% agora.
Você pode ver facilmente por que isso ocorre se comparar os gráficos abaixo. Em ambos os casos, temos distribuições com a mesma diferença: uma unidade: a distribuição laranja tem média zero (0) e a distribuição vermelha tem média um (1). Contudo, neste primeiro gráfico, o desvio padrão de ambas as distribuições é igual a um (1), de modo que elas se soprepõem em grande parte. Encontrar esse efeito, portanto, é bem difícil, daí ser necessário uma amostra maior para isso.
require(ggplot2)
ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
stat_function(fun = dnorm, n = 1000, args = list(mean = 0, sd = 1), color = "orange") +
geom_vline(aes(xintercept = 0), color = "orange", linetype = "dashed", alpha = 0.4) +
stat_function(fun = dnorm, n = 1000, args = list(mean = 1, sd = 1), color = "red") +
geom_vline(aes(xintercept = 1), color = "red", linetype = "dashed", alpha = 0.4) +
ylab("") + xlab("") +
scale_y_continuous(breaks = NULL) +
scale_x_continuous(limits = c(-3, +4), breaks = seq(from = -2, to =4, by =1)) +
theme_classic()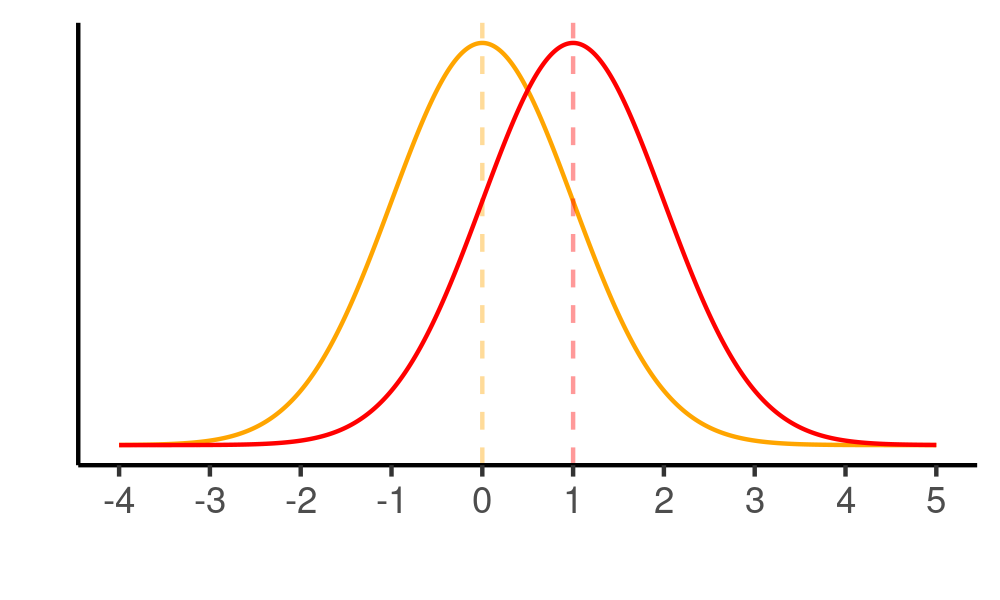
Neste segundo caso, reduzimos o desvio padrão em um quarto (de 1 para 0.25), de modo que as distribuições quase não se sobrepõem. Assim sendo, apesar de a diferença entre elas continuar sendo a mesma (1), ficou muito mais fácil achar um efeito aqui, de modo que precisamos de uma amostra menor para isso.
ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
stat_function(fun = dnorm, n = 1000, args = list(mean = 0, sd = 0.25), color = "orange") +
geom_vline(aes(xintercept = 0), color = "orange", linetype = "dashed", alpha = 0.4) +
stat_function(fun = dnorm, n = 1000, args = list(mean = 1, sd = 0.25), color = "red") +
geom_vline(aes(xintercept = 1), color = "red", linetype = "dashed", alpha = 0.4) +
ylab("") + xlab("") +
scale_y_continuous(breaks = NULL) +
scale_x_continuous(limits = c(-1, 2), breaks = seq(from = -1, to = 2, by = 1)) +
theme_classic()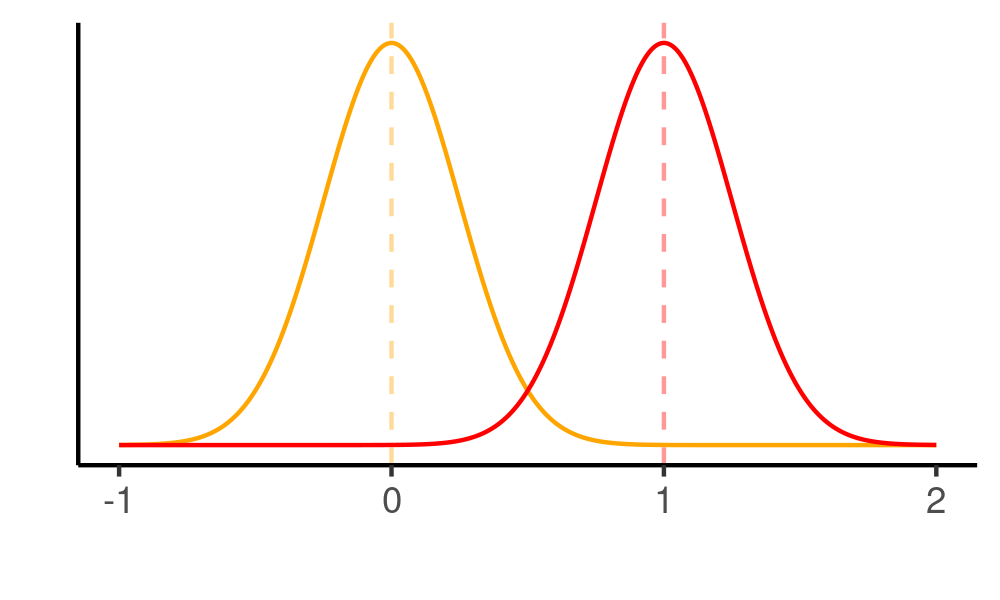
Exemplo 7: O poder do teste e o nível de significância
Vamos fazer uma pequena mudança na nossa função e acrescentar mais um argumento a ela, o parâmetro alpha, de modo que possamos brincar com o nível de significância.
poder.paired2 <- function(n, mu1, mudiff, sigma1, sigma2, rho12, nsims, alpha){
nsims = nsims
# vetor vazio para armazenar os valores de p
pvalor <- c()
for(i in 1:nsims){
n = n
mu1 = mu1
mudiff = mudiff
sigma1 = sigma1
sigma2 = sigma2
rho12 = rho12
mu2 <- mu1 + mudiff # define a média da segunda condição
# Definir a matriz de covariância
cov12 <- rho12 * sigma1 * sigma2
vcov <- matrix(c(sigma1^2, cov12,
cov12, sigma2^2), nrow=2, byrow=T)
# Realizandoo procedimento de amostragem
head(Y <- rmvnorm(n, c(mu1, mu2), vcov))
Y1 <- Y[, 1]
Y2 <- Y[, 2]
test <- t.test(Y2, Y1, paired = T)
pvalor <- c(pvalor, test$p.value)
}
dados <- as.data.frame(pvalor)
poder <- dados %>%
summarise(poder = sum(pvalor < alpha) / nsims)
ggplot() +
geom_density(data = dados, aes(x = pvalor), fill = "orange", color = "orange", alpha = 0.4) +
geom_vline(aes(xintercept = 0.05), color = "red", linetype = "dashed") +
geom_segment(aes(x = 0.05, xend = alpha, y = 0.35, yend = 0.35),
color = "grey", arrow = arrow(length = unit(0.03, "npc"))) +
geom_vline(aes(xintercept = alpha), color = "blue", linetype = "dashed") +
geom_text(data = poder, aes(label = poder, x = alpha*1.5, y = 0.2), color = "blue") +
theme_classic() +
labs(x = "p-valor", y = "Densidade")
}Vamos esatabeler um nível de significância igual a 0.1, ou seja, 10% (indicado pela linha azul no gráfico. A linha vermelha continua indicando 5% ou 0.05). Se fazemos isso, estamos aumentando a área de rejeição da hipótese nula e, portanto, aumentando o poder do teste. Logo, teremos mais p-valores que consideramos significativos e, portanto, maior poder.
poder.paired2(n = 50,
mu1 = 150,
mudiff = 10,
sigma1 = 40,
sigma2 = 40,
rho12 = 0.3,
nsims = 1000,
alpha = 0.1)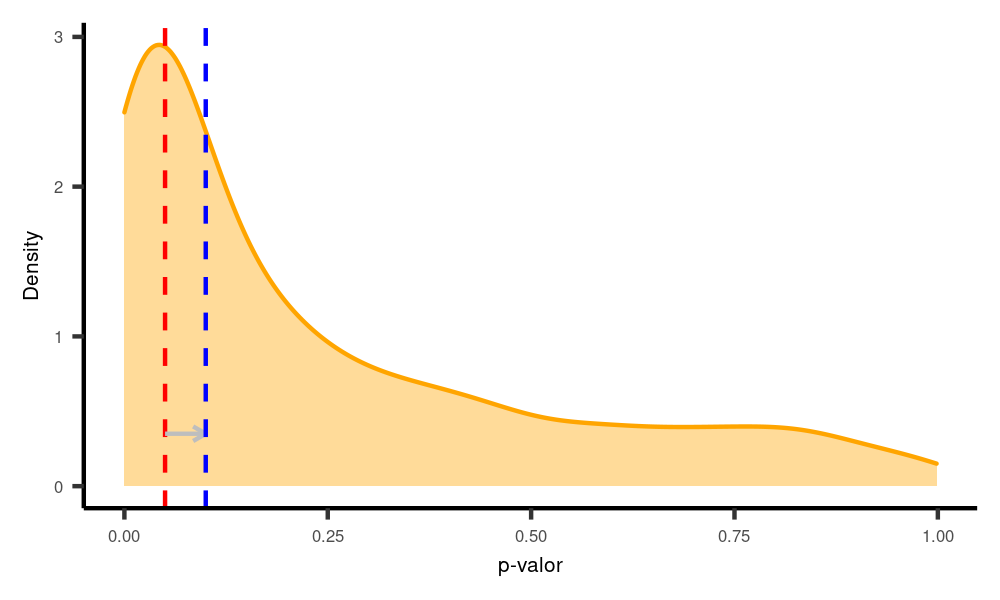
O inverso ocorre se diminuirmos o nível de significância. Nesse caso, reduzimos o poder e, logo, a probabilidade de encontrar um efeito quando ele de fato existe. Vamos testar com alpha 0.01 (1%):
poder.paired2(n = 50,
mu1 = 150,
mudiff = 20,
sigma1 = 20,
sigma2 = 20,
rho12 = 0.3,
nsims = 1000,
alpha = 0.01)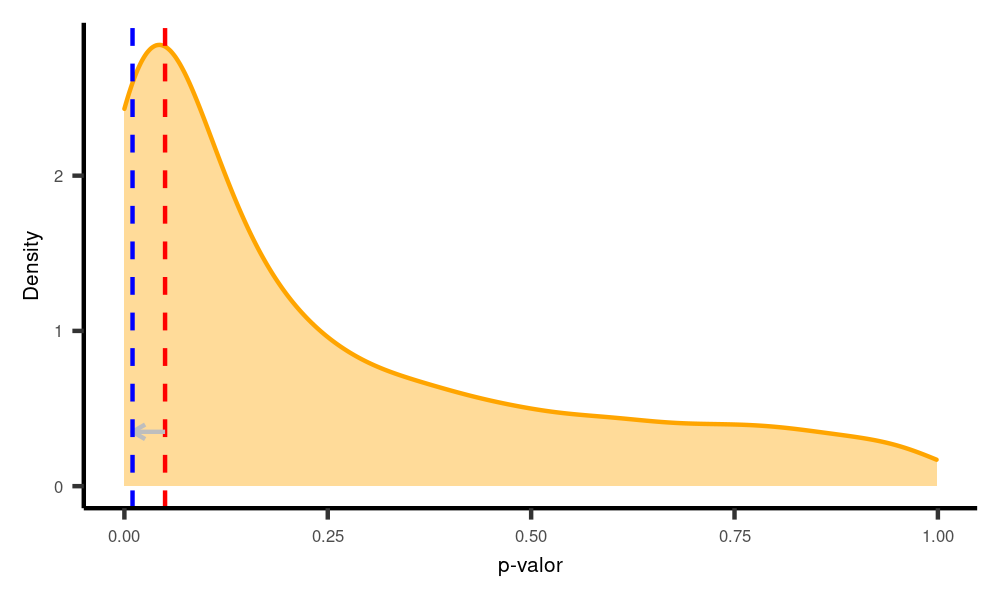
Esse ponto é muito importante, pois mostra que o p-valor e o poder do teste são informações relacionados. Logo, não faz qualquer sentido calcular o poder do teste depois que o p-valor foi calculado (o chamado poder post-hoc ou poder calculado). O poder necessariamente tem de ser calculado antes da realização do experimento.
Agora que entendemos os conceitos basilares por detrás da noção de poder estatístico, podemos avançar para os modelos mistos e como calcular o poder para eles.